Homework #6
EE 364: Spring 2026
Assigned: 17 February Due: Tuesday, 24 February at 16:00
BrightSpace Assignment: Homework 6
Write your solutions to these homework problems. Submit your work to BrightSpace by the due date. Show all work and box answers where appropriate. Do not guess.
Problem 0
Daily derivation #6, Derive all the BEG-CUP pdf moments: binomial, geometric, hypergeometric, negative binomial, Poisson, gamma, exponential, chi-square, beta, uniform, Gaussian.
Problem 1
Let \(A\) be an event. Define the indicator function \[I_A(x) = \begin{cases} 1 & \textrm{if } x \in A \\ 0 & \textrm{if } x \notin A. \end{cases}\]
Evaluate \(I_A(x) + I_{A^C}(x)\).
Compute \(E[I_A]\).
Prove: \(E[X] \ge E[X \cdot I_{\{X \ge c\}}]\) for any constant \(c\) and any positive random variable \(X\) with \(E[X] < \infty\).
Problem 2
Let \(Y = A \, \cos(\omega t) + c\) where \(\omega\) and \(c\) are constants with \(E[A] = \mu\) and \(V[A] = \sigma^2\). Find the mean and variance of \(Y\).
Problem 3
Find the mean and variance of \(X\) if
\[f_X(x) = \begin{cases} c (1-x^2) & -1 \le x \le 1 \\ 0 & \textrm{else}. \end{cases}\]
\[f_X(x) = \begin{cases} c x (1-x^2) & 0 \le x \le 1 \\ 0 & \textrm{else}. \end{cases}\]
Problem 4
Suppose that \(B\) and \(C\) are standard uniform random variables, i.e. \(B \sim U[0,1]\) and \(C \sim U[0,1]\). Calculate \(E[B^n]\) and \(V[B^n]\).
Problem 5
A dart is equally likely to land at any point inside a circular target of radius 2. Let \(R\) be the distance of the landing point from the origin. Find the mean and variance of \(R\).
Problem 6
Random variable \(X\) equals 2 with probability \(0.4\) and is uniformly distributed \([0, 1]\) otherwise. What is \(E[X] + V[X]\)?
Problem 7
Suppose that \(A\) and \(B\) each randomly and independently choose 3 of 10 objects. Find the expected number of objects,
chosen by both \(A\) and \(B\).
not chosen by either \(A\) or \(B\).
chosen by exactly one of \(A\) and \(B\).
Problem 8
Let \(Z \sim N(0, 1)\). Define \(Y = Z + n\) for some constant \(n\). Compute \(E[Y^6]\).
Problem 9
Random variable \(X \sim N(0, 4)\). What is \(E[|X|]\)?
Problem 10
Suppose \(Y\) is a non-negative random variable.
Show: \(\displaystyle E[Y] = \int_{0}^{\infty} P(Y > t) dt\).
Show: \(\displaystyle E[Y^n] = \int_{0}^{\infty} n \, x^{n-1} P(Y > x) dx\).
Problem 11
Random variable \(X_1 \sim N(0, 1)\). Define \(X_i \sim N(X_{i-1}, 1)\). What is the distribution of \(X_n\)?
Problem 12
Let \(X\) be a Pareto random variable, \(f_X(x) = \frac{2}{x^3}\) for \(x \ge 1\), and \(f(x)=0\) otherwise.
Compute \(E[X]\).
Compute \(E[X^2]\).
Problem 13
Let \(X\) be a Poisson random variable with parameter \(\lambda\). Show directly that \(E[X^n] = \lambda E[( X + 1 )^{n - 1}]\). Use the result to compute \(E[X^3]\).
Problem 14
Suppose that \(X\) is a random variable with pdf \[f_X(x) = \begin{cases} a + b x^2 & 0 \le x \le 1 \\ 0 & \textrm{ else}. \end{cases}\] Find \(a\) and \(b\) if \(E[X] = \frac{3}{5}\).
Problem 15
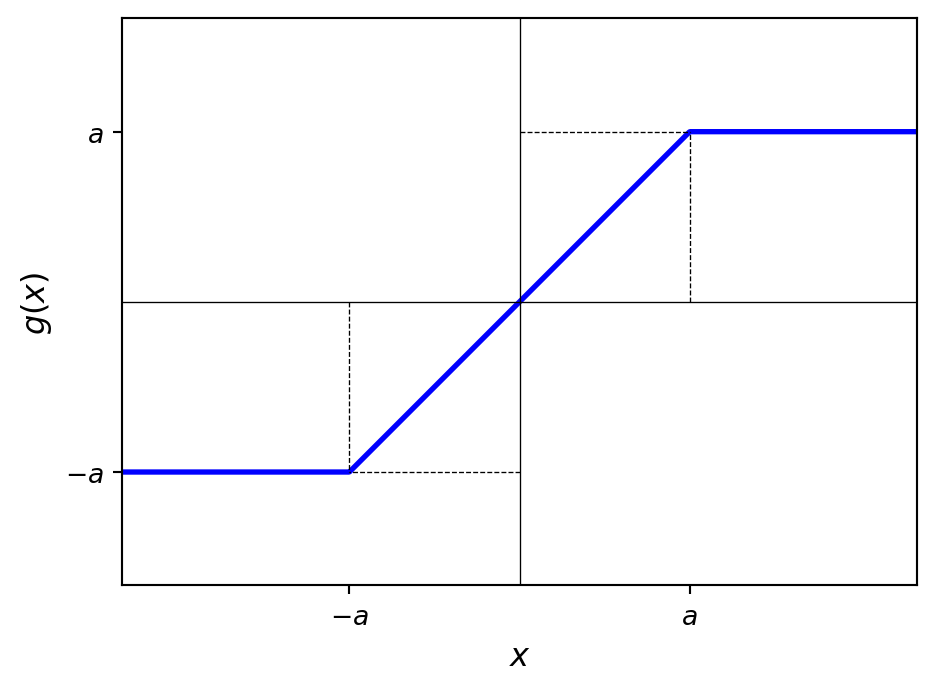
Consider the following limiter, \(g(x)\):
Find expressions for the mean and variance of \(Y = g(X)\) for an arbitrary continuous random variable \(X\) with symmetric pdf, \(f_X(x)\).
Suppose \(a = 1\). Evaluate the mean and variance if \(X\) is a Laplacian random variable with \(\lambda = 1\), that is \(f_X(x) = \frac{1}{2 \lambda} \exp\left(-\frac{|x|}{\lambda}\right)\).
Suppose \(a = \frac12\). Evaluate the mean and variance if \(X = U^3\) where \(U \sim U[-1, 1]\).
Problem 16
Consider the following limiter with center-level clipping, \(h(x)\):
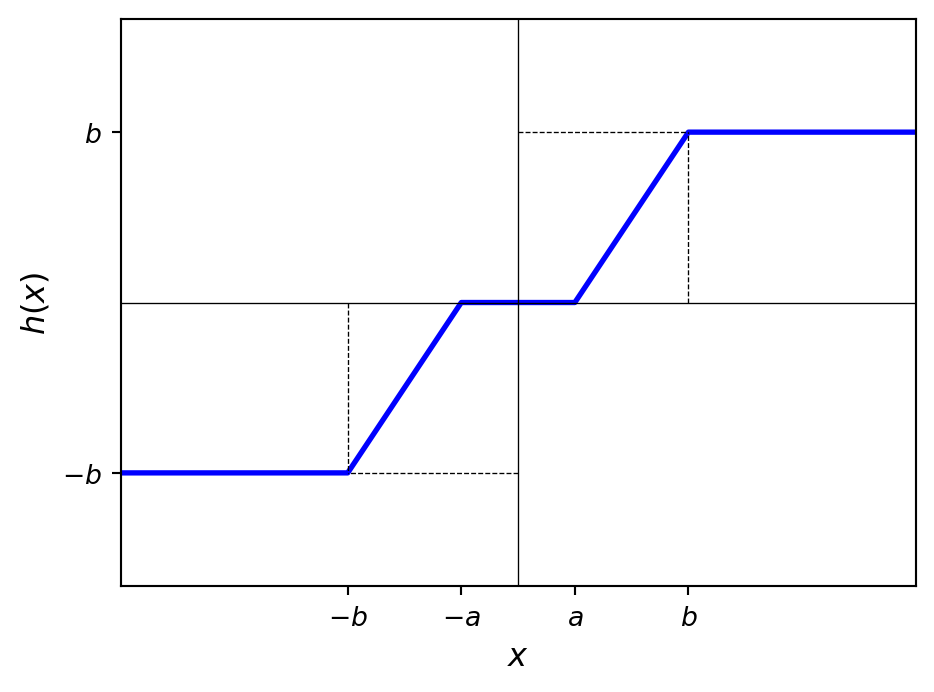
Find expressions for the mean and variance of \(Y = h(X)\) for an arbitrary continuous random variable \(X\) with symmetric pdf, \(f_X(-x) = f_X(x)\).
Suppose \(a = 1\) and \(b = 2\). Evaluate the mean and variance if \(X\) is a Laplacian random variable with \(\lambda = 1\), that is \(f_X(x) = \frac{1}{2 \lambda} \exp\left(-\frac{|x|}{\lambda}\right)\).
Suppose \(a = \frac12\) and \(b = \frac34\). Evaluate the mean and variance if \(X = b \cos(2 \pi U)\) where \(U \sim U[-1, 1]\).